你有没有想过,数学的世界里,函数的单调性就像是一首美妙的乐曲,时而高亢激昂,时而低沉婉转。今天,就让我带你走进这个奇妙的世界,一起探索函数单调性的奥秘吧!
一、什么是函数的单调性?
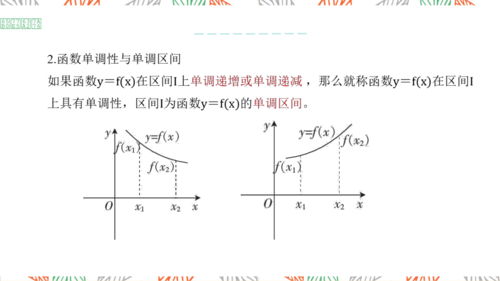
首先,得弄明白什么是函数的单调性。简单来说,就是函数在某个区间内,要么一直上升,要么一直下降。就像爬山一样,要么一路向上,要么一路向下,不会出现一会儿上坡一会儿下坡的情况。
二、单调性的分类

函数的单调性主要有两种:单调递增和单调递减。
单调递增:函数在某个区间内,随着自变量的增大,函数值也不断增大。就像爬楼梯,一步比一步高。
单调递减:函数在某个区间内,随着自变量的增大,函数值却不断减小。就像下楼梯,一步比一步低。
三、如何判断函数的单调性?
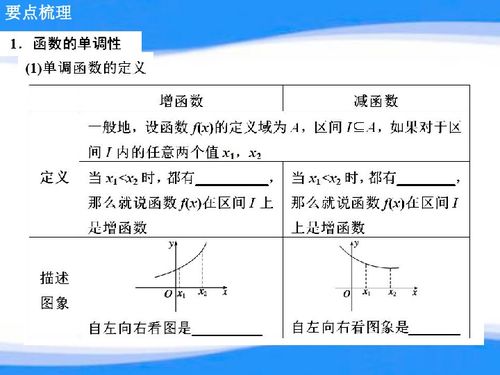
判断函数的单调性,主要有两种方法:
定义法:根据函数单调性的定义,直接判断函数在某个区间内是单调递增还是单调递减。
导数法:利用导数的性质,判断函数在某个区间内是单调递增还是单调递减。
四、导数法详解
导数法是判断函数单调性的常用方法。下面,我们就来详细了解一下。
1. 求导数:首先,对函数求导,得到导数表达式。
2. 判断导数的正负:判断导数在某个区间内的正负。
如果导数恒大于0,那么函数在该区间内单调递增。
如果导数恒小于0,那么函数在该区间内单调递减。
如果导数在某个区间内既有正值又有负值,那么函数在该区间内不具有单调性。
五、实例分析
为了更好地理解函数的单调性,我们来举几个例子。
例1:判断函数$f(x) = x^2$在区间$[0, 1]$上的单调性。
解:首先,对函数求导,得到导数$f'(x) = 2x$。判断导数在区间$[0, 1]$上的正负。由于$x$在区间$[0, 1]$上恒大于0,所以导数恒大于0。因此,函数$f(x) = x^2$在区间$[0, 1]$上单调递增。
例2:判断函数$f(x) = -x^2$在区间$[-1, 1]$上的单调性。
解:首先,对函数求导,得到导数$f'(x) = -2x$。判断导数在区间$[-1, 1]$上的正负。由于$x$在区间$[-1, 1]$上既有正值又有负值,所以导数在区间$[-1, 1]$上既有正值又有负值。因此,函数$f(x) = -x^2$在区间$[-1, 1]$上不具有单调性。
通过以上分析,相信你已经对函数的单调性有了更深入的了解。在这个美妙的世界里,函数的单调性就像是一首美妙的乐曲,等待着我们去欣赏、去探索。让我们一起走进数学的世界,感受函数单调性的魅力吧!







